Research

My research is focused on investigating various processes in kinetic plasma physics through theory and computation, with occasional comparisons to observational/experimental data for guidance and validation. To this end, I apply fully-kinetic VPIC simulations and/or Hybrid VPIC simulations (where the electrons are treated as a fluid and ions are advanced with VPIC’s particle-in-cell implementation) to study systems such as magnetic mirrors, astrophysical explosions, and magnetic reconnection sites relevant to Earth’s magnetosphere. Sometimes a simulation will help to formulate a theoretical model, and other times simulations are run with the intention of validating a model or matching some physically measured data. Sections below cover several applications of interest with which I have worked.

Magnetic Reconnection

Magnetic reconnection is the process by which magnetic energy is converted to particle energy through a topological rearrangement of magnetic field lines, and it is thought to be involved in a host of plasma phenomena including solar flares, coronal mass ejections, and the generation of terrestrial aurorae. Though a ubiquitous process, the underlying dynamics of magnetic reconnection are not yet well understood. Several fluid models exist to explain reconnection, but are generally insufficient in explaining a process that is innately intertwined with small-scale kinetic physics (which is based on statistical distribution functions).

Computational simulation is vital to understanding magnetic reconnection, as it complements experimental observation with superior data resolution and access to a larger region of parameter space. For magnetic reconnection, the kinetic models required to capture full electron and ion dynamics necessitate the use of high performance computing, as billions of particles regularly cross over domains and constant communication is needed between cores. My research goal is to use VPIC fully-kinetic simulations to model collisionless magnetic reconnection and elucidate its underlying dynamics.

Drift-kinetic gradients and agyrotropy

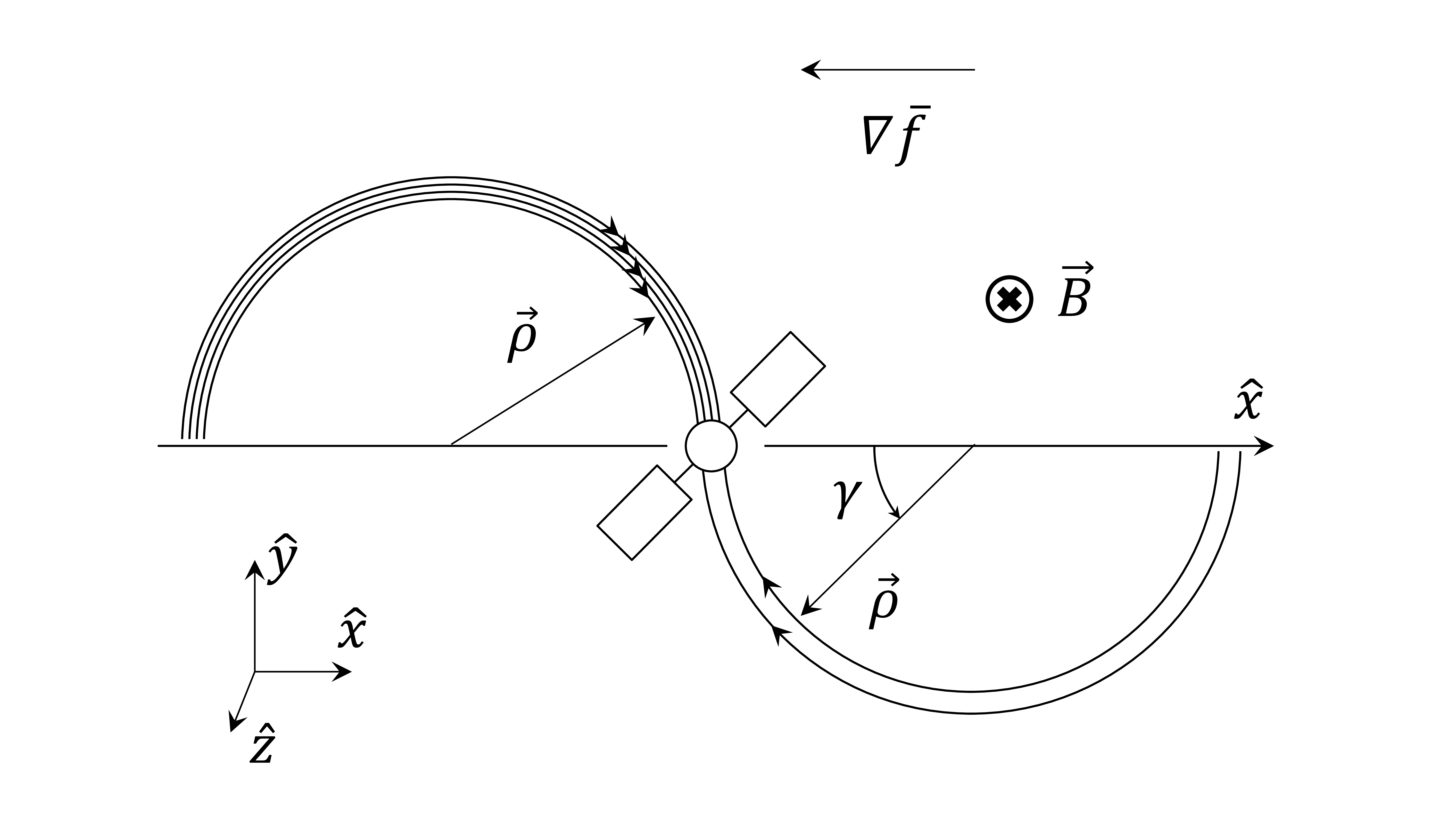
My research often focuses on collisionless plasma physics. Collisions function to maintain isotropy in the velocity space distribution of a plasma component. In a magnetized collisionless plasma, this means that the dynamics parallel to the local magnetic field can become decoupled from those in the perpendicular plane, leading to anisotropic pressure tensors. This is important in the inflows of collisionless magnetic reconnection, and is the foundation of many of the projects I have worked on. When further nonideal processes are included, the two directions perpendicular to the local magnetic field can decouple. This is called agyrotropy, and it is often taken to be an indicator of particles demagnetizing. One of my favorite projects to date is the development of a drift-kinetic method for determining gradients in plasma properties based on local measurements of the velocity space distribution function. The work establishes a fundamental connection between gradients in plasma properties and agyrotropy in the distribution function. The figure below illustrates the basic principle of how this works, and a paper is now published on the formal theory, which is based in drift-kinetics and applies vector calculus liberally to estimate gradients in arbitrary moments of the distribution function based on local measurements. The final arXiv version of that paper can be found here.

Magnetic Mirrors

The axisymmetric magnetic mirror was one of the first fusion reactor concepts, in part due to its simple geometry relative to the Tokamaks and stellarators that dominate the conversation in magnetically confined fusion today. Initial interest in magnetic mirrors was largely doused by poor electron confinement due to large end losses of nearly parallel traveling particles. Additionally, the simple mirror is unstable to curvature-driven magnetohydrodynamic (MHD) interchange modes, although this can be mitigated through several approaches. Magnetic mirrors confine charged particles via the mirror force on magnetized particles. The mirror contains a central region with B strong enough to remain magnetized and confined, with end regions of stronger B to reflect particles inward. Particles traveling nearly parallel to the magnetic field lines will not be confined by the mirror, making the device inherently lossy. Confinement depends on having a large mirror ratio (the ratio of the values of the magnetic field strength at the reflecting cusps and in the central confining cell) while the minimum of B is still strong enough to maintain magnetization of the fastest ions in the central region. As such, being able to retain large magnetic fields is important. The advent of High Temperature Superconducting (HTS) magnets and some promising developments from the GDT experiment in Russia warrant a new look at mirrors.

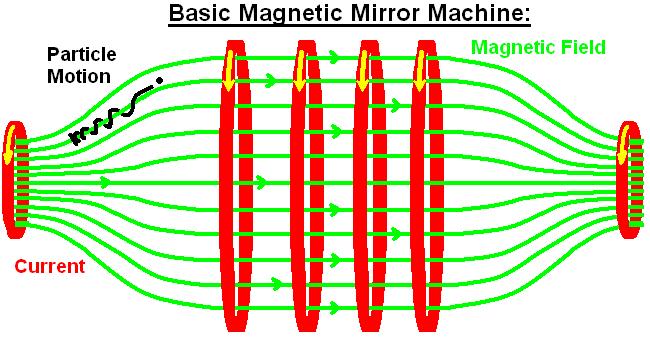
We have developed a drift-kinetic model to explain electron parallel confinement in the expander region of a magnetic mirror, focusing on distinct orbit types to explain the form of the electron and ion distributions encountered in the expander. This model captures the essential physics of the ambipolar potential in the expander with negligible computational cost for realistic devices, which would be difficult to simulate in a fully-kinetic regime. More on this model and the simulations used to validate it can be found in the arXiv version of this PoP paper.

More recently, we have begun modeling full mirror devices in both the fully-kinetic and hybrid codes, including the effects of injected fast ions in a weakly collisional regime.